A) 2.8
B) 4.67
C) 3.4
D) 5.67
F) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
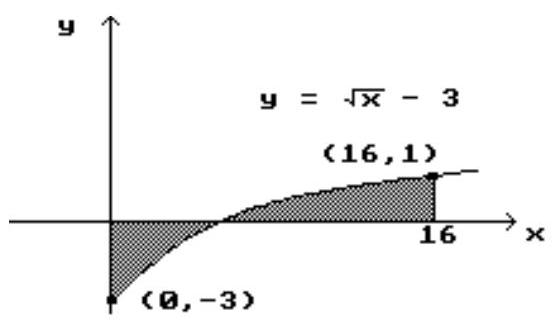
Find the area of the shaded region.
-
A)
B)
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area bounded by the given curves. - and
A) 14.619
B) 2.569
C) 46.379
D) 9.730
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the integral. -
A)
B)
C)
D)
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area bounded by the given curves. -
A)
B)
C)
D)
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the integral. -
A)
B)
C)
D)
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the integral. -
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use integration by parts to find the integral. -
A)
B)
C)
D)
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the integral. -
A)
B)
C)
D)
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate the definite integral. -
A) 0.0160
B) -0.0024
C) -0.0080
D) 0.0040
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use integration by parts to find the integral. -
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the given indefinite integral. -
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The work (in joules) done by a force (in newtons) moving an object through a distance (in meters) is given by . Find a formula for , if and is a constant.
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the integral. -
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Work the exercise. -Find the total revenue function (in thousands of dollars) if the marginal revenue (in thousands of dollars per unit) at a production level of units is , and .
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the integral. -
A)
B)
C)
D)
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Provide an appropriate response. -If we use as a substitution to find , then which of the following would be the correct results? i. ii) iii)
A) i is correct.
B) iii is correct.
C) ii is correct.
D) None of these is correct.
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the particular solution of the differential equation. - when
A)
B)
C)
D)
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the integral. -
A)
B)
C)
D)
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the particular solution of the differential equation. - when
A)
B)
C)
D)
F) C) and D)
Correct Answer

verified
Correct Answer
verified
Showing 81 - 100 of 227
Related Exams