FiltersDone

Question type

Essay

Multiple Choice

Short Answer

True False

Matching

Exam 14: Describing Relationships: Scatterplots and Correlation

Show Answer

Share

---

All types

Filters

Study FlashcardsPractice ExamLearn

Question 21

Multiple Choice

Review LaterAdd Note

Review Later

You read that "the correlation between spending on schools (dollars per pupil) and median score on student achievement tests is r = 0.08." This means that

A) school districts that spend a lot have higher scores than low-spending districts, and this effect is quite strong.
B) school districts that spend a lot have lower scores than low-spending districts, and the effect is quite strong.
C) school districts that spend a lot have somewhat higher scores than low-spending districts, but the effect is weak.
D) school districts that spend a lot have somewhat lower scores than low-spending districts, but the effect is weak.

E) None of the above
F) B) and C)

Correct Answer

verified

Show Answer

Question 22

Multiple Choice

Review LaterAdd Note

Review Later

Consider the following data: 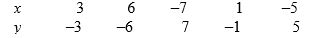The correlation coefficient r is

A) 7.6.
B) 0.0
C) 1.0.
D) -0.6.
E) -1.0.

F) A) and B)
G) B) and D)

Correct Answer

verified

Show Answer

Question 23

Multiple Choice

Review LaterAdd Note

Which of the following pairs of variables is most likely to show a positive correlation?

A random sample of statistics students was selected. The heights (inches) and the weights (pounds) of the students were collected and are displayed in the figure below. 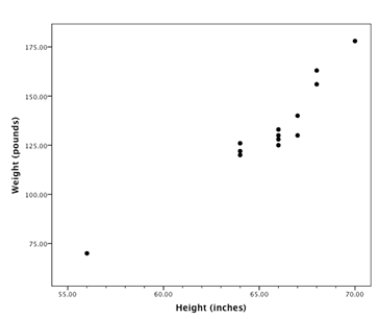There is a student whose measurements were outliers in the data set. The height of this student was about

An analyst gathers data on the number of hours of political debates watched per week and the sales of antacids. She expects that political debate watching will help explain antacid sales. In a scatterplot of her data:

Which correlation indicates almost no straight-line relationship?

To display the relationship between per capita yearly liquor consumption and liver disease death rates per 100,000 people in each of 29 countries, a good choice of a graph would be a:

A nutrition study measured how many helpings of vegetables each of 125 grade school children were served each week during a school year and their body mass index (BMI) scores. Which variable would one put on the horizontal axis of a scatterplot of the data?

The correlation between two variables is of -0.18. One can conclude that:

The scout troop is selling brownies for $4 per plate (no sales tax.) If the explanatory variable was the number of plates of brownies a customer purchased and the response was the amount paid, what would be the correlation between the number of plates and amount paid?

Which of the following statements about correlation is false?

A study found that the size of the police force and the number of churches in towns across the United States are positively associated. This means that:

Which of the following are most likely to be positively correlated?

An agricultural economist says that the correlation between corn prices and rainfall during the growing season is r = -0.7. This means that:

You calculate the correlation between height and weight for a simple random sample of 50 students from your college. Another student does the same for a simple random sample of 200 students from the college. The other student should get

A random sample of patients who attended a clinic was selected. The age of the patient (years) and the number of days since the last visit were collected and are displayed in the figure. 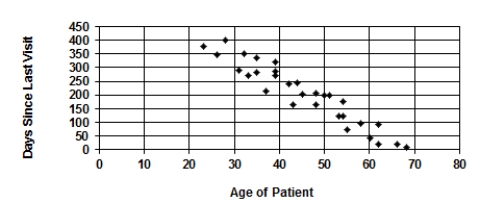A plausible value of the correlation coefficient for the data displayed is

A study is conducted to determine if there is a relationship between height (inches) and annual income (dollars) among executives at large companies in the United States. Which of the following statements about the descriptive statistics for the study data is not true?

A study of home heating costs collects data on the size of houses and the monthly cost to heat the houses with natural gas. Here are the data: A friend tells you that the correlation for the data is r = 0.99984. You conclude from this number that

How well does the number of beers a student drinks predict his or her blood alcohol content? Sixteen student volunteers at The Ohio State University drank a randomly assigned number of cans of beer. Thirty minutes later, a police officer measured their blood alcohol content (BAC) . A scatterplot of the data appears below. 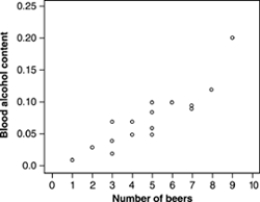The scatterplot above shows

A random sample of patients who attended a clinic was selected. The age of the patient (years) and the number of days since the last visit were collected and are displayed in the figure. Describe the association between "Age of Patient" and "Days Since Last Visit."